How to create a bounding volume for a set of vertices, Pt 1: Capsules (with Unity implementation)
Creating some sort of bounding volume for a set of vertices is a common problem in simulations and games. Capsules, or swept spheres, are a powerful option to use as a bounding volume because of how little data is required to define them and how quickly they can be checked for collision detection. Imagine taking a sphere and sweeping it along a single line in space; the shape of this would be a capsule. We can define a capsule then as:
Vector3 start;
Vector3 end;
float radius;
These techniques can be used on any sort of point cloud, but let’s state the specifics of our case. We have a set of vertices that define some bone (right forearm, left leg, hip, etc.) and we want to find a capsule that best fits them. We’ll show how to do this generically and then how to adapt it to use Unity components.
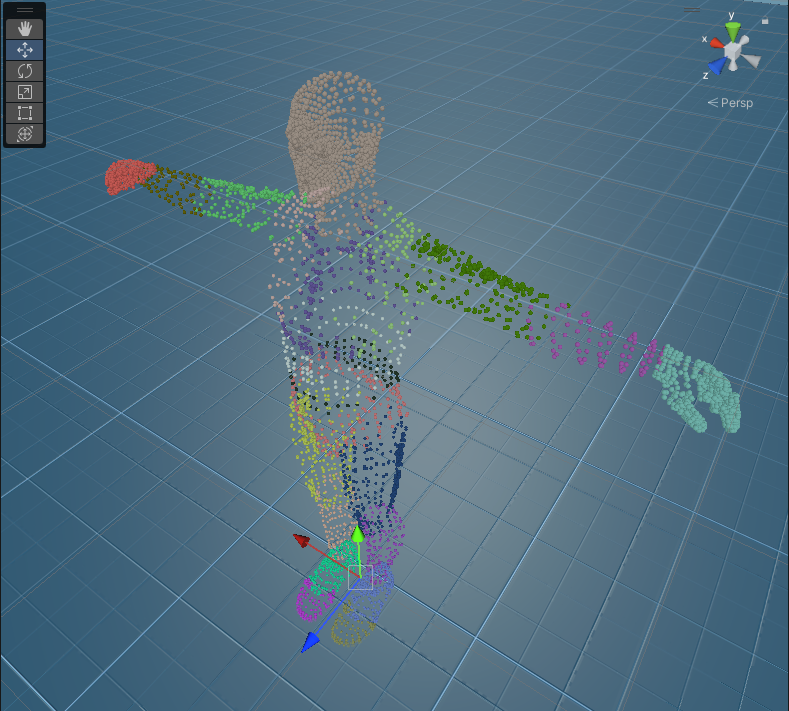
Let’s think about this problem visually. We want to find an axis that explains as much variance of the vertex set as possible so we can use that as the line we sweep our sphere on. We also want to find a secondary axis that captures (as much as possible) of the rest of the variance in the set. Luckily there’s a pretty straightforward, standard way of doing this: Principal Component Analysis (PCA). Thankfully this only requires an undergrad level of linear algebra to to understand.
The primary and secondary axes I just referred to can be evaluated as the eigenvectors of the covariance matrix of the vertex set. That’s a mouthful, so let’s break it down.
Covariance
The covariance of two variables is the amount they vary together - if the greater values of x tend to occur with the greater values of y, then the covariance is positive. If the greater values of x tend to occur with the lesser values of y, then it is negative. If there’s no correlation, it should be close to zero.
\(cov_{x,y}=\frac{1}{N} \sum_{i=1}^{N}(x_{i}-\bar{x})(y_{i}-\bar{y})\)
where \(\bar{x}\) and \(\bar{y}\) are the means of the respective values
A covariance matrix is a handy way of capturing how much each dimension varies with every other dimension. So in the case of vertices, which are Vector3s, we have a 3x3 covariance matrix:
| x | y | z | |
|---|---|---|---|
| x | covar(x,x) | covar(x,y) | covar(x,z) |
| y | covar(y,x) | covar(y,y) | covar(y,z) |
| z | covar(z,x) | covar(z,y) | covar(z,z) |
The entries on the diagonal are the covariance of a variable with itself, which is the same as its variance. You might also notice this matrix is symmetrical. That is an important property we will exploit later.
However, for our case this simple calculation of covariance might not be sufficient. We need to consider how this applies to our data. For one, we don’t want to consider interior points - we’re only interested in the points that define the shell of our volume. To be specific, we want to make sure our vertices form a convex hull.
Luckily, most meshes are by definition convex hulls. However, the data defining the mesh can still be skewed in a way that messes up our calculation. For example, for the upper left leg, there are a lot more vertices around the inside groin area than any other part of the surface, so our primary axis can end up looking like this:
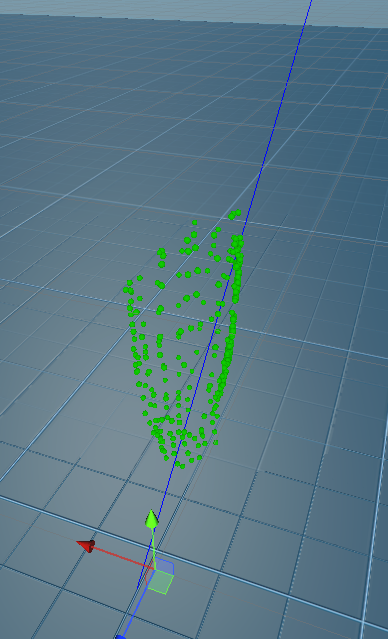
In order to prevent this, we can use the continuous formulation for covariance, shown below, and do some culling on tightly grouped vertices before hand:
Continous Covariance [1]
Given \(n\) triangles \((p_{k}, q_{k}, r_{k})\), \(0 \le k < n\), in the convex hull, the covariance matrix is given by
\(cov_{i,j}=(\frac{1}{a_{H}} \sum_{k=1}^{n}\frac{a_{H}}{12}(9m_{k,i}m_{k,j} + p_{k,i}p_{k,j} + q_{k,i}m_{k,j} + r_{k,i}r_{k,j}) ) - m_{H,i}m_{H,j}\)
where \(a_{k} = \Vert (q_{k} - p_{k}) \times (r_{k} - p_{k}) \Vert / 2\) is the area and \(m_{k} = (p_{k} + q_{k} + r_{k}) / 3\) is the centroid of triangle k
The total area of the convex hull is given by \(a_{H} = \sum_{k=1}^{n}a_{k}\)
and the centroid of the convex hull, \(m_{H} = \frac{1}{a_{H}}\sum_{k=1}^{n}a_{k}m_{k}\)
is computed as the mean of the triangle centroids weighted by the area.
Let’s see how this looks implemented into code:
// Rudimentary algorithm to filter out a bunch of verts that are close to each other
public static Vector3[] filter_verts(Vector3[] verts, float min_rad, ref bool[] kept)
{
int n = verts.Length;
bool[] keep = Enumerable.Repeat(true, n).ToArray();
kept = keep;
int num_kept = verts.Length;
while (true)
{
bool should_break = true;
for(int i = 0; i < n; i++)
{
if (!keep[i])
continue;
for (int j = 0; j < n; j++)
{
if (!keep[j] || i == j)
continue;
if (Vector3.Distance(verts[i], verts[j]) < min_rad)
{
keep[i] = false;
num_kept--;
should_break = false;
break;
}
}
}
if (should_break)
break;
}
Vector3[] new_verts = new Vector3[num_kept];
int new_verts_idx = 0;
for (int i = 0; i < n; i++)
if (keep[i])
new_verts[new_verts_idx++] = verts[i];
return new_verts;
}
public static double[,] calculate_continous_covar(Mesh mesh)
{
int[] triangles = mesh.triangles;
Vector3[] verts = mesh.vertices;
double[,] covar = new double[3, 3];
float total_area = 0f;
Vector3 mesh_centroid = Vector3.zero;
Vector3 a, b, c;
for (int i = 0; i < triangles.Length; i += 3)
{
a = verts[triangles[i]];
b = verts[triangles[i + 1]];
c = verts[triangles[i + 2]];
float area = triangle_area(a, b, c);
total_area += area;
mesh_centroid += triangle_centroid(a, b, c) * area;
}
mesh_centroid /= total_area;
float get_vector_idx(Vector3 v, int idx)
{
if (idx == 0)
return v.x;
else if (idx == 1)
return v.y;
else if (idx == 2)
return v.z;
throw new Exception($"Interal function incorrectly accesssed - get_centroid_idx: {idx}" );
}
for (int i = 0; i < 3; i++)
{
for (int j = 0; j < i + 1; j++)
{
float covar_ij = 0;
for (int k = 0; k < triangles.Length; k += 3)
{
a = verts[triangles[k]]; b = verts[triangles[k + 1]]; c = verts[triangles[k + 2]];
float area = triangle_area(a, b, c);
Vector3 centroid = triangle_centroid(a, b, c);
float term_1 = 9 * get_vector_idx(centroid, i) * get_vector_idx(centroid, j);
float term_2 = get_vector_idx(a, i) * get_vector_idx(a, j) + get_vector_idx(b, i) * get_vector_idx(b, j) + get_vector_idx(c, i) * get_vector_idx(c, j);
covar_ij += (area / 12f) * (term_1 + term_2);
}
covar_ij /= total_area;
covar_ij -= get_vector_idx(mesh_centroid, i) * get_vector_idx(mesh_centroid, j);
covar[i, j] = covar_ij;
covar[j, i] = covar_ij;
}
}
return covar;
}
public static float triangle_area(Vector3 a, Vector3 b, Vector3 c)
{
Vector3 ba = b - a;
Vector3 ca = c - a;
Vector3 cross = Vector3.Cross(ba, ca);
return cross.magnitude / 2;
}
public static Vector3 triangle_centroid(Vector3 a, Vector3 b, Vector3 c)
{
return (a + b + c) / 3;
}
Now let’s see how our primary axis will look
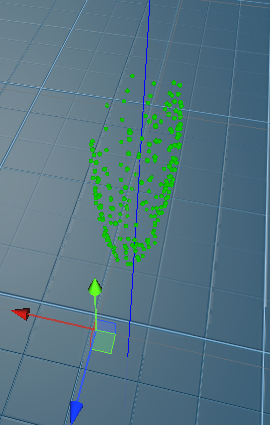
Much better! But how do we get that primary axis?
Eigenvectors are our friend
The eigenvectors of a matrix are an important concept in linear algebra. A matrix is a transformation of space, and eigenvectors are special in that when the matrix transformation of space occurs, these vectors will point in the same direction, and will only be scaled by a scalar value - their corresponding eigenvalue.
There are a ton of ways to compute eigenvectors; usually, I would recommend power iteration [2], as it is the simplest to implement. However, our matrix is symmetrical, so there exists a direct formula for calculating the eigenvalues [3]. There’s a lot of code in this next block, but most of it is the implementation of basic matrix operations.
public static double det(double[,] x)
{
return x[0, 0] * x[1, 1] * x[2, 2] +
x[0, 1] * x[1, 2] * x[2, 0] +
x[0, 2] * x[1, 0] * x[2, 1] -
x[0, 2] * x[1, 1] * x[2, 0] -
x[0, 1] * x[1, 0] * x[2, 2] -
x[0, 0] * x[1, 2] * x[2, 1];
}
public static double[,] matrix_scalar_mult(double[,] mat, double n)
{
double[,] ans = new double[3, 3];
for (int i = 0; i < 3; i++)
for (int j = 0; j < 3; j++)
ans[i, j] = mat[i, j] * n;
return ans;
}
// equivalent to A - nI where I is the identity matrix
public static double[,] subtract_n_times_identity(double[,] mat, double n = 1)
{
double[,] ans = new double[3, 3];
for (int i = 0; i < 3; i++)
for (int j = 0; j < 3; j++)
if (i == j)
ans[i, j] = mat[i, j] - n;
else
ans[i, j] = mat[i, j];
return ans;
}
// Given a real symmetric 3x3 matrix A, compute the eigenvalues
// Note that acos and cos operate on angles in radians
public static double[] get_eigenvalues(double[,] mat)
{
double[] eigenvalues = new double[3];
double p1 = Math.Pow(mat[0, 1], 2) + Math.Pow(mat[0, 2], 2) + Math.Pow(mat[1, 2], 2);
if (Mathf.Approximately((float)p1, 0))
return new double[] { mat[0, 0], mat[1, 1], mat[2, 2] };
double q = trace(mat) / 3;
double p2 = Math.Pow(mat[0, 0] - q, 2) + Math.Pow(mat[1, 1] - q, 2) + Math.Pow(mat[2, 2] - q, 2) + 2 * p1;
double p = Math.Sqrt(p2 / 6);
double[,] B = matrix_scalar_mult(subtract_n_times_identity(mat, q), 1 / p);
double r = det(B) / 2;
// In exact arithmetic for a symmetric matrix - 1 <= r <= 1
//but computation error can leave it slightly outside this range.
double phi;
if (r <= -1)
phi = Math.PI / 3;
else if (r >= 1)
phi = 0;
else
phi = Math.Acos(r) / 3;
// the eigenvalues satisfy eig3 <= eig2 <= eig1
double eig1 = q + 2 * p * Math.Cos(phi);
double eig3 = q + 2 * p * Math.Cos(phi + (2 * Math.PI / 3));
double eig2 = 3 * q - eig1 - eig3; // since trace(A) = eig1 + eig2 + eig
eigenvalues[0] = eig1;
eigenvalues[1] = eig2;
eigenvalues[2] = eig3;
return eigenvalues;
}
With these eigenvalues we can calculate the corresponding eigenvectors. Again, we can exploit the symmetry of our covariance matrix and use this algorithm to calculate the corresponding eigenvector for a given eigenvalue:
// mat must be normal (for real mat this means symmetric)
public static Vector3 get_eigenvector_from_value(double[,] mat, double eigenvalue)
{
double[,] x = subtract_n_times_identity(mat, eigenvalue);
// The cross product of two ind. col of x will be in the null space
// that is, it will be an eigenvector associated with the eigenvalue
if (are_ind_cols(x, 0, 1))
{
double[] t = cross(x, 0, 1, true);
return new Vector3((float)t[0], (float)t[1], (float)t[2]);
}
else if (are_ind_cols(x, 0, 2))
{
return Vector3.Cross(col_to_vec(x, 0), col_to_vec(x, 2));
}
else if (are_ind_cols(x, 1, 2))
{
return Vector3.Cross(col_to_vec(x, 1), col_to_vec(x, 2));
}
if (mat_is_zero(x))
return Vector3.zero;
int col_idx = col_is_zero(x, 0) ? (col_is_zero(x, 1) ? 2 : 1) : 0;
// Suppose v is a non zero column of x
// Choose an arbitrary vector u not parallel to v
// Then v x u will be perpinduclar to v and thus will be eigenvectors of the eigenvalue
Vector3 v = col_to_vec(x, col_idx);
Vector3 u = new Vector3(v.x, v.y, v.z) + Vector3.forward;
return Vector3.Cross(v, u);
}
public static double[] cross(double[,] mat, int col_a_idx, int col_b_idx, bool _normalize = false)
{
double[] a = new double[] { mat[0, col_a_idx], mat[1, col_a_idx], mat[2, col_a_idx] };
double[] b = new double[] { mat[0, col_b_idx], mat[1, col_b_idx], mat[2, col_b_idx] };
var product = new double[] {a[1] * b[2] - a[2] * b[1],
a[2] * b[0] - a[0] * b[2],
a[0] * b[1] - a[1] * b[0] };
if (_normalize)
normalize(product);
return product;
}
public static void normalize(double[] x)
{
double sqrMag = x.Aggregate(0d, (sum, cur) => sum + cur * cur);
double mag = Math.Sqrt(sqrMag);
for (int i = 0; i < x.Length; i++)
x[i] /= mag;
}
public static bool col_is_zero(double[,] mat, int col_idx)
{
for (int i = 0; i < mat.GetLength(0); i++)
if (!Mathf.Approximately((float)mat[i, col_idx], 0))
return false;
Debug.Log($"Column {col_idx} is zero");
return true;
}
public static bool mat_is_zero(double[,] mat)
{
for (int i = 0; i < mat.GetLength(0); i++)
for (int j = 0; j < mat.GetLength(1); j++)
if (!Mathf.Approximately((float)mat[i, j], 0))
return false;
return true;
}
public static Vector3 col_to_vec(double[,] arr, int col_idx)
{
return new Vector3((float)arr[0, col_idx], (float)arr[1, col_idx], (float)arr[2, col_idx]);
}
public static bool are_ind_cols(double[,] mat, int col_a_idx, int col_b_idx)
{
double[] col_a = new double[] { mat[0, col_a_idx], mat[1, col_a_idx], mat[2, col_a_idx] };
double[] col_b = new double[] { mat[0, col_b_idx], mat[1, col_b_idx], mat[2, col_b_idx] };
if (col_is_zero(mat, col_a_idx) || col_is_zero(mat, col_b_idx))
{
return false;
}
double factor = col_b[0] / col_a[0];
for (int i = 1; i < 3; i++)
if (!Mathf.Approximately((float)(col_a[i] * factor), (float)col_b[i]))
return true;
Debug.Log($"Col idx {col_a_idx} and {col_b_idx} have factor {factor}");
return false;
}
Great! Now we have the primary and secondary axes - but we still don’t know where the sweeping line should start and end. In order to find the length of the primary axis, we can project all the points onto the primary axis and find the maximum distance between any two points. So far I have been referring to the largest eigenvector as the primary axis, but we need two points to define a line, so we’ll use the mean of the vertices as the other point.
For the radius, we could select a value large enough that all the points are inside the capsule, but these vertices should really define the surface of the capsule. To find a good radius, we should find a value that minimizes the sum of the squared distances from the vertices to the surface of the capsule. This is the same as the mean of the distances of the vertices to the principal axis [4]
public static float get_max_dist_apart(Vector3[] verts, ref Vector3 center)
{
// O(n) method to test: since we know they'll be on a line determined by a and b,
// we can set a to go through the origin and shift all other points by subtracting a
// from them. Then, we know that that the min and max magnitudes represent the furthest
// apart points
float ans = float.NegativeInfinity;
for (int i = 0; i < verts.Length; i++)
for (int j = i + 1; j < verts.Length; j++)
if ((verts[i] - verts[j]).magnitude > ans) {
ans = (verts[i] - verts[j]).magnitude;
center = (verts[i] + verts[j]) / 2;
}
return ans;
}
public static Vector3[] proj_verts_onto_axis(Vector3[] verts, Vector3 point_a, Vector3 point_b)
{
Vector3[] proj_verts = new Vector3[verts.Length];
for (int i = 0; i < verts.Length; i++)
{
proj_verts[i] = closest_point_on_line(point_a, point_b, verts[i]);
}
return proj_verts;
}
// Projects point b onto line defined by a and b
public static Vector3 closest_point_on_line(Vector3 a, Vector3 b, Vector3 p)
{
Vector3 ap = p - a;
Vector3 ab = b - a;
Vector3 result = a + Vector3.Dot(ap, ab) / Vector3.Dot(ab, ab) * ab;
return result;
}
Putting it all together
Now that we have all the functionality we need, we can finally write the function to generate the bounding box. In order to implement this in Unity, we also need to work around the constraints of the CapsuleCollider. Unity doesn’t allow you to set the rotation outright. In order to get around this, we can attach the collider to a child GameObject and change the rotation of that object’s transform. The rotation needs to be a quaternion that takes the capsule’s direction (we’ll keep it to the default x-axis) and orients it onto the line defined by our start and end points. The final code looks like:
// Returns Quat Q such that v1 * q = v2
public static Quaternion get_rot_between(Vector3 v1, Vector3 v2)
{
Vector3 dir_vec = v2.normalized;
Vector3 a = Vector3.Cross(v1, dir_vec);
float w = Mathf.Sqrt(dir_vec.sqrMagnitude * v1.sqrMagnitude) + Vector3.Dot(dir_vec, v1);
Quaternion q = new Quaternion(a.x, a.y, a.z, w);
return q.normalized;
}
public static GameObject calc_bounding_capsule(Vector3[] verts, int bone_id)
{
int n = verts.Length;
Vector3 mean = calc_mean(verts);
SkinnedMeshRenderer rend = GetComponent<SkinnedMeshRenderer>();
Mesh mesh = rend.sharedMesh;
double[,] covar = calculate_continous_covar(mesh);
double[] eigenvalues = get_eigenvalues(covar);
Vector3 largest_eigen = get_eigenvector_from_value(covar, eigenvalues[0]).normalized;
Vector3[] proj_verts = proj_verts_onto_axis(verts, mean, mean + largest_eigen);
Vector3 center = Vector3.zero;
float height = get_max_dist_apart(proj_verts, ref center);
double dist_from_main_axis_sum = 0;
foreach (Vector3 v in verts)
dist_from_main_axis_sum += (v - closest_point_on_line(mean, mean + largest_eigen, v)).magnitude;
float radius = (float)dist_from_main_axis_sum / n;
GameObject capsuleObject = new GameObject();
capsuleObject.transform.position = center;
capsuleObject.transform.rotation = get_rot_between(Vector3.right, largest_eigen);
CapsuleCollider capsule = capsuleObject.AddComponent<CapsuleCollider>();
capsule.height = height;
capsule.direction = 0;
capsule.radius = radius;
return capsuleObject;
}
And here’s what our final character looks like! I used [5] to generate capsule meshes that fit the capsule colliders, modified the shoulder capsules by hand, and used boxes for the feet:
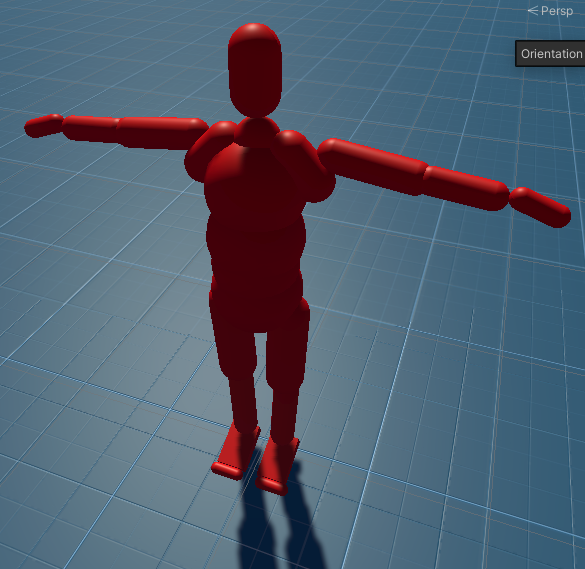
Also, you may have noticed we only ended up needing the largest eigenvalue. That’s because for a capsule, the radius will be orthogonal to our principal axis. The other eigenvectors are useful for calculating Oriented Bounding Boxes (OBBs) - we’ll go over how to do that in part 2 of this blog :)
[1] Christer Ericson. 2004. Real-Time Collision Detection. CRC Press, Inc., USA.
[2] A good overview of power iteration: https://jakerice.design/2018/09/19/Covariance-and-Principal-Component-Analysis/
[3] https://en.wikipedia.org/wiki/Eigenvalue_algorithm - see section on symmetric 3x3 matrices
[4] Two proofs of this (a) https://stats.stackexchange.com/questions/520286/how-can-i-prove-mathematically-that-the-mean-of-a-distribution-is-the-measure-th
(b) https://math.stackexchange.com/questions/1766713/showing-that-mean-of-vectors-minimizes-the-sum-of-the-squared-distances
[5] See AlucardJay’s reply: https://forum.unity.com/threads/solved-closed-procedurally-generated-capsule.406982/